Jak obliczyć długość krokwi dach jednospadowy – wzory

Redakcja 2025-04-29 01:06 / Aktualizacja: 2026-01-20 01:49:41 | Udostępnij:

Planujesz dach jednospadowy i chcesz uniknąć drogich pomyłek w zakupie drewna? Pomyśl o prostocie tej konstrukcji, gdzie jedna pochyła płaszczyzna spoczywa na ścianach różnej wysokości. Omówimy kluczowe parametry wejściowe, wzory trygonometryczne jak L/cos(α) i pitagorejski, oraz jak precyzyjnie doliczyć zwis okapu, uwzględniając normy wytrzymałościowe dla stabilności.

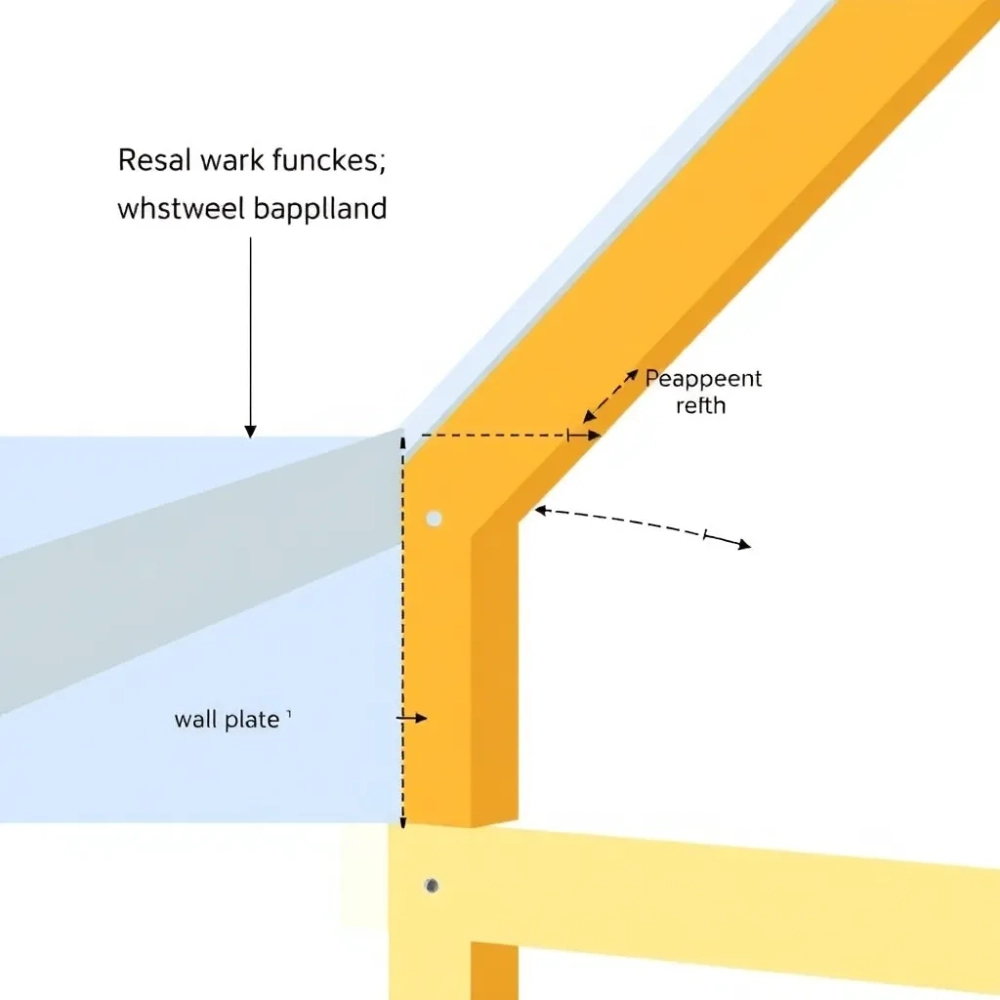
Jak obliczyć długość krokwi dach jednospadowy

Parametry wejściowe do długości krokwi jednospadowej

Dach jednospadowy wymaga trzech głównych danych: szerokości przęsła L, czyli odległości między ścianami nośnymi, kąta nachylenia α oraz zwisu okapu z. Szerokość L mierzy się poziomo na rzucie płaskim, zazwyczaj od 3 do 6 metrów bez dodatkowych podpór. Kąt α określa spadek, wpływając na wytrzymałość pod śniegiem. Zwis z to 30-50 cm, chroniący elewację przed wodą.

Przygotuj miarkę i kalkulator trygonometryczny. L koryguj o grubość murłaty i izolacji. α podawaj w stopniach, korzystając z aplikacji mobilnych. Z zawsze sprawdzaj lokalne przepisy budowlane.

  • Szerokość L: pozioma odległość ścian.
  • Kąt α: 15-45° dla większości pokryć.
  • Zwis z: min. 30 cm dolny, górny zależny od α.

Wzór trygonometryczny krokwi: L / cos(α)

Najprostszy wzór na długość krokwi Lk to L podzielone przez cosinus kąta α. W trójkącie prostokątnym L stanowi przyprostokątną, a Lk przeciwprostokątną do α. Dla L=4 m i α=30°, cos(30°)=0,866, więc Lk=4/0,866≈4,62 m. Ten wzór działa bezpośrednio z rzutu płaskiego.

Zobacz także: Jakie krokiew na dach jednospadowy: wymiary i dobór

Użyj kalkulatora naukowego lub Excela z funkcją COS(). Wprowadź α w radianach po konwersji (α*PI()/180). Unikniesz błędów zaokrągleń, mnożąc przez 100 i dzieląc na końcu.

Norma PN-EN 1995-1-1 zaleca weryfikację pod obciążenia, ale wzór geometryczny jest uniwersalny dla wstępnych obliczeń.

Długość krokwi Pitagorasem: √(L² + H²)

Alternatywa to wzór Pitagorasa: Lk=√(L² + H²), gdzie H to wysokość spadku. Najpierw oblicz H, potem podnieś do kwadratu obie składowe. Dla L=5 m, H=2 m, Lk=√(25+4)=√29≈5,39 m. Idealny, gdy znasz różnicę wysokości ścian.

Zobacz także: Jakie krokwie na dach jednospadowy 5m – przekrój i rozstaw

Ten sposób sprawdza się w programach CAD, wizualizując trójkąt. Pitagoras potwierdza trygonometrię, minimalizując błędy pomiarowe.

Obliczenie wysokości spadku H = L × tan(α)

Wysokość spadku H mnoży L przez tangens α. Tangens(α) to stosunek przeciwprostokątnej do przyprostokątnej. Dla α=25°, tan(25°)≈0,466, więc przy L=4,5 m H=2,1 m. To podstawa do Pitagorasa.

Użyj TAN() w Excelu. H decyduje o różnicy ścian, wpływając na stabilność konstrukcji.

Sprawdź normy: H min. dla kątów zgodnych z pokryciem.

Doliczanie zwisu okapu do krokwi jednospadowej

Dolny zwis dodaj prosto: Lk całkowita = Lk + z. Górny zwis koryguj: z / sin(α), bo wydłuża po skosie. Dla z=40 cm, α=30°, sin(30°)=0,5, dodatek=80 cm.

  • Dolny okap: +z poziomo.
  • Górny: +z/sin(α).

Całkowita długość decyduje o zakupie belek.

Kąt nachylenia α dla krokwi dach jednospadowy

Kąt α dobierz wg norm PN-EN 1995-1-1: min. 5° blachodachówka, 15° ceramika. Uwzględnij strefę śniegową i wiatr. Dla Polski typowo 20-35°.

Wzrost α znacząco wydłuża krokwie, wymagając wzmocnień powyżej 4 m.

Wskazówki pomiarowe długości krokwi jednospadowej

Mierz L na poziomie krokwi, nie gruntu – dodaj grubość muru. Użyj niwelatora dla α. Weryfikuj w programach jak arkusze z tabelami cos/tan.

Dla drewna max 4-6 m bez słupków; dłuższe dziel kobyłkami. Konsultuj konstruktora pod normy wytrzymałościowe.

Testuj model 3D dla stabilności.

Pytania i odpowiedzi

  • Jak obliczyć długość krokwi dla dachu jednospadowego? Długość krokwi (Lk) oblicza się jako hipotenusę trójkąta prostokątnego: Lk = L / cos(α), gdzie L to szerokość przęsła (odległość między ścianami), a α to kąt nachylenia dachu w stopniach. Alternatywnie: Lk = √(L² + H²), gdzie H = L × tan(α). Użyj kalkulatora lub tabel trygonometrycznych.

  • Jakie dane wejściowe są potrzebne do obliczenia długości krokwi? Podstawowe parametry to: szerokość przęsła L, kąt nachylenia α (15-45°), zwis okapu z (30-50 cm). Mierz L na poziomie krokwi, korygując o grubość muru i murłaty. Weryfikuj programami jak Krokiew lub arkuszami Excel.

  • Jak uwzględnić zwis okapu w długości krokwi? Całkowita długość = Lk + z / sin(α) dla górnego zwisu lub Lk + z dla dolnego okapu. Zawsze dodaj zwis po obliczeniu podstawowej Lk, aby zapewnić stabilność konstrukcji.

  • Jakie są minimalne kąty nachylenia dachu jednospadowego? Według norm PN-EN 1995-1-1: min. 5° dla blachodachówek, 15° dla dachówek ceramicznych. Dla dłuższych krokwi (powyżej 4-6 m) stosuj wzmocnienia jak kobyłki. Konsultuj z konstruktorem.